A tour of probabilistic programming language APIs

Introduction

I wanted an easy reference for myself and others to see how different developers think about defining probabilistic models, and this is an attempt at that. I have a number of biases I am a contributor to PyMC3, and have been working on PyMC4 (which uses TensorFlow probability). I write far more Python than R, and far more R than julia or C++. , but the code shown here is open-source, and contributions/suggestions are gratefully accepted.

I am also including an opinionated - but I hope fair - summary of the projects as of the time of writing. On my TODO list are greta in R; Turing and Gen in Julia; and Figaro and Rainier in Scala. Different libraries are written for different reasons, and I care strongly about easily writing and sharing models, and then sampling from them.

The Task

I have generated a dataset as follows:

import numpy as np

np.random.seed(0)

ndims = 5
ndata = 100
X = np.random.randn(ndata, ndims)
w_ = np.random.randn(ndims)  # hidden
noise_ = 0.1 * np.random.randn(ndata)  # hidden

y_obs = X.dot(w_) + noise_

For each probabilistic programming language (PPL), I will:

1. Write down the following model: $$ \begin{align} p(\mathbf{w}) &\sim \mathcal{N}(\mathbf{0}, I_5)\\ p(\mathbf{y} | X, \mathbf{w}) &\sim \mathcal{N}(X\mathbf{w}, 0.1I_{100}), \end{align} $$ where \(I_n\) is the \(n \times n\) identity matrix.
2. Draw 1,000 samples from the posterior distribution $$ p(\mathbf{w} | X, \mathbf{y}) \propto p(\mathbf{y} | X, \mathbf{w}) p(\mathbf{w}) $$ where I pass y_obs to the code at some point.
3. Do a sanity check that the samples for w are reasonable near to the true values for w, given the model.For those keeping track at home, the posterior of the model given the data is also a Gaussian, $$p(\mathbf{w} | X, \mathbf{y}) = \mathcal{N}((X^TX + I_5)^{-1}X^T\mathbf{y}, (X^TX + I_5)^{-1})$$

PyStan

Documentation for PyStan, and for Stan itself.

Hand-rolled automatic differentiation in C++. Many (most?) good ideas in PyMC3 came from here. Updates to the code sometimes accompany papers describing the new algorithms. The authors/contributors care deeply about correctness and practicality, and it shows. A very good, fast choice if you care about MCMC. The models are in their own programming language, which can be a little funny to use in Python (where I would prefer Python objects to strings). Uses the dynamic NUTS algorithmThe Stan team actually keeps changing/improving the sampling algorithm they use, and calling it NUTS is at least a little misleading, since these improvements are substantive compared to the algorithm described in the paper. If you want to be proper, call it something like "dynamic Hamiltonian Monte Carlo method with multinomial sampling of dynamic length trajectories, generalized termination criterion, and improved adaptation of the Euclidean metric." by default, which is currently the best default to use, though only two libraries here have a good version.

import pystan

linear_regression = """
data {
  int N;   // number of data items
  int K;   // number of predictors
  matrix[N, K] X;   // predictor matrix
  vector[N] y;      // outcome vector
}
parameters {
  vector[K] w;       // coefficients for predictors
}
model {
  y ~ normal(X * w, 0.1);  // likelihood
}
"""

linear_data = {'N': ndata,
               'K': ndims,
               'y': y_obs,
               'X': X}

sm = pystan.StanModel(model_code=linear_regression)
fit = sm.sampling(data=linear_data, iter=1000, chains=4)

PyMC3

Documentation.

Uses theano for automatic differentiation. The contributors are strong, all the diagnostics are good looking, and all the estimates are above average See my biases above.. More seriously, it is quite fast, flexible if you are willing to write Theano, and has robust tuning and diagnostics, so you can get some samples from a model with a minimum of fuss. Interoperates quite smoothly with Python projects. Also uses the NUTS algorithm.

import pymc3 as pm
import theano.tensor as tt

with pm.Model():
    w = pm.Normal('w', 0, 1, shape=ndims)
    y = pm.Normal('y', tt.dot(X, w), 0.1, observed=y_obs)
    trace = pm.sample(1000)

emcee

Documentation.

This library is a "pure-Python implementation of Goodman & Weare’s Affine Invariant Markov chain Monte Carlo (MCMC) Ensemble sampler", and does not use gradients. This means it does not scale as well to over, say 10 dimensions, but installation is very easy. Also somewhat unique in writing custom likelihood and prior density functions. Lots of examples and users in the astrophysics community.

import scipy.stats as st

import emcee

# log likelihood
def lnlike(w, X, y):
    model = X.dot(w)
    inv_sigma2 = 0.1 ** -2
    return -0.5*(np.sum((y-model)**2)*inv_sigma2 - np.log(inv_sigma2))

# Define a prior for w
w_rv = st.multivariate_normal(np.zeros(ndims), np.eye(ndims))

# Log probability for w
lnprior = w_rv.logpdf

# logp(w | X, y) = logp(y | X, w) + logp(w)
def lnprob(w, X, y):
    return lnprior(w) + lnlike(w, X, y)

nwalkers = 100
pos = w_rv.rvs(size=nwalkers)
sampler = emcee.EnsembleSampler(nwalkers, ndims, lnprob, args=(X, y_obs))

pos, lprob, rstate  = sampler.run_mcmc(pos, 1000)

Pyro

Documentation.

Uses pytorch for automatic differentiation. I get the impression the library traditionally cared more about variational inference, but running HMCAs is the case with TensorFlow Probability, this implementation is parametrized by number of steps rather than path length, which has some performance implications I still do not entirely grasp. For example, taking smaller steps with a fixed path length means each sample takes longer, while keeping a fixed number of steps means the sample will take the same amount of time but be more correlated. was quite smooth. There is no NUTS, which means you may have to manually set the number of stepsThis was clearly documented, I just missed it. Updated the code example to use it, too.. Pyro implements NUTS as well as HMC.

import pyro
import torch
from pyro.infer.mcmc import NUTS, MCMC
import pyro.distributions as dist


def model(X):
    w = pyro.sample('w', dist.Normal(torch.zeros(ndims), torch.ones(ndims)))
    y = pyro.sample('y', dist.Normal(torch.matmul(X, w), 0.1 * torch.ones(ndata)),
                    obs=torch.as_tensor(y_obs, dtype=torch.float32))
    return y

nuts_kernel = NUTS(model, adapt_step_size=True)
py_mcmc = MCMC(nuts_kernel, num_samples=1_000, warmup_steps=500)

py_mcmc = py_mcmc.run(torch.as_tensor(X, dtype=torch.float32))

TensorFlow Probability

Documentation.

Uses tensorflow for automatic differentiation. This is also using raw HMC parametrized by number of steps (see Pyro for commentary). This is the most verbose of the libraries reviewed here, which can be good (more control) and bad (this was four lines in PyMC3)I actually had a bug for a while where I had w_dist = tfd.Normal(loc=tf.zeros(ndims), scale=1.0, name="w"). This defines a valid model, because tfp is so flexible, but the wrong model.. The computations are also all vectorized: I can sample 1,000 chains in about the same time I sample 4 chains, which seems pretty unique.Blog post coming on that. These are some reasons why one might write a high level, user friendly API on top of this library and name it PyMC4.

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

X_tensor = tf.convert_to_tensor(X, dtype='float32')

@tf.function
def target_log_prob_fn(w):
    w_dist = tfd.Normal(loc=tf.zeros((ndims, 1)), scale=1.0, name="w")
    w_prob = tf.reduce_sum(w_dist.log_prob(w))
    y_dist = tfd.Normal(loc=tf.matmul(X_tensor, w), scale=0.1, name="y")
    y_prob = tf.reduce_sum(y_dist.log_prob(y_obs.reshape(-1, 1)))
    return w_prob + y_prob


# Initialize the HMC transition kernel.
num_results = 1000
num_burnin_steps = 500
adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
    tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn=target_log_prob_fn,
        num_leapfrog_steps=4,
        step_size=0.01),
    num_adaptation_steps=int(num_burnin_steps * 0.8))

samples, is_accepted = tfp.mcmc.sample_chain(
    num_results=num_results,
    num_burnin_steps=num_burnin_steps,
    current_state=tf.zeros((ndims, 1)),
    kernel=adaptive_hmc,
    trace_fn=lambda _, pkr: pkr.inner_results.is_accepted)

Edward 2

Documentation.

Uses tensorflow for automatic differentiation. This is a submodule of TensorFlow Probability that provides a flexible API based on the ideas from the popular Edward libraryThe same developer, so the similarity is not surprising.. Note the biggest change from the tfp code above is that defining the joint probability is a bit cleaner, but we still use the same code to actually get the samples.

from tensorflow_probability import edward2 as ed
import tensorflow as tf

X_tensor = tf.convert_to_tensor(X, dtype='float32')

def linear_regression(X):
    w = ed.Normal(loc=tf.zeros((ndims, 1)), scale=1.0, name="w")
    y = ed.Normal(loc=tf.matmul(X, w), scale=0.1, name='y')
    return y

log_joint = ed.make_log_joint_fn(linear_regression)


def target_log_prob_fn(w):
    return log_joint(X_tensor, w=w, y=y_obs.reshape(-1, 1))

# Below here is from TFP section
num_results = 1000
num_burnin_steps = 500

adaptive_hmc = tfp.mcmc.SimpleStepSizeAdaptation(
    tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn=target_log_prob_fn,
        num_leapfrog_steps=4,
        step_size=0.01),
    num_adaptation_steps=int(num_burnin_steps * 0.8))

ed_samples, is_accepted = tfp.mcmc.sample_chain(
    num_results=num_results,
    num_burnin_steps=num_burnin_steps,
    current_state=tf.zeros((ndims, 1)),
    kernel=adaptive_hmc,
    trace_fn=lambda _, pkr: pkr.inner_results.is_accepted)

Numpyro

Documentation.

Uses jax for automatic differentiation. Built by the same people who work on Pyro, and includes a very cool iterative implemenation of the NUTS algorithmI have not looked closely enough to see if this is "NUTS as in the 2013 paper", or "NUTS as in the algorithm implemented by Stan/PyMC3.". Note the import section looks a little overwhelming, but jax is a wonderful library that wraps numpy functionality. A more typical usage would be to import jax.numpy as np, so that no one was any wiser that you are using autodiff. This looks very similar to the Pyro implementation, but notice I am jumping through fewer hoops to convert my numpy arrays into torch tensors.

import jax.numpy as jnp
from jax import random

import numpyro.distributions as dist
from numpyro.handlers import sample
from numpyro.hmc_util import initialize_model
from numpyro.mcmc import mcmc


def model(X):
    w = sample('w', dist.Normal(jnp.zeros(ndims), jnp.ones(ndims)))
    y = sample('y', dist.Normal(jnp.matmul(X, w), 0.1 * jnp.ones(ndata)), obs=y_obs)

rng = random.PRNGKey(0)

init_params, potential_fn, constrain_fn = initialize_model(rng, model, X=X)
num_warmup, num_samples = 1000, 2000

# Run NUTS.
npyro_samples = mcmc(num_warmup, num_samples, init_params,
                 potential_fn=potential_fn,
                 trajectory_length=10,
                 constrain_fn=constrain_fn)

Brancher

Documentation.

NOTE: Very new library. As far as I can tell, this does not implement MCMC (yet?), nor can I calculate log probabilities to verify my implementation. It looks nice, though!

Uses pytorch for automatic differentiation. This came out this week, and I gave it a test drive, but could not do much damage with it yet.

from brancher.variables import ProbabilisticModel
from brancher.standard_variables import NormalVariable
from brancher import inference
import brancher.functions as BF
import torch

X_tensor = torch.as_tensor(X, dtype=torch.float32)

# Model
w = NormalVariable(loc=torch.zeros(ndims), scale=1., name="w")
y = NormalVariable(loc=BF.matmul(X_tensor, w), scale=0.1, name="y")

y.observe(y_obs)
model = ProbabilisticModel([w, y])

PyMC4

Documentation.

NOTE: Still working on the API. Don't use this yet.

Uses tensorflow probability (and hence TensorFlow) for automatic differentiation. I am including this for what the model definition syntax is looking like right now, though some work needs to happen to wire the model through to the proper TensorFlow Probability functions.

import pymc4
import tensorflow as tf

@pymc4.model()
def linear_model():
    w = yield pymc4.distributions.Normal('w', mu=np.zeros((5, 1)), sigma=1.)
    y = yield pymc4.distributions.Normal('y', mu=tf.matmul(X, w), sigma=0.1)

PyProb

Documentation.

Joins emcee in not using a gradient based sampler -- here we use importance sampling. I also had to cheat a little bit and take 50,000 samples instead of 1,000 to get the estimates to be reasonable. The samples are pretty fast, but I suspect this does not scale to higher dimensionsNow I have a paper to read about how importance sampling can scale. (but I also suspect that this does allow for defining a more broad class of models than most of the other languages). Defining this model was pretty nice, and I am surprised more languages do not subclass a Model object.

import torch

import pyprob
from pyprob import Model
from pyprob.distributions import Normal


class LinearModel(Model):
    def forward(self):
        X_tensor = torch.as_tensor(X, dtype=torch.float32)

        w = pyprob.sample(Normal(torch.zeros(ndims), torch.ones(ndims)))
        y = Normal(torch.matmul(X_tensor, w), 0.1 * torch.ones(ndata))

        pyprob.observe(y, name='y_obs')
        return w

model = LinearModel()

posterior = model.posterior_distribution(
    num_traces=50_000,
    inference_engine=pyprob.InferenceEngine.IMPORTANCE_SAMPLING,
    observe={'y_obs': torch.as_tensor(y_obs, dtype=torch.float32)})

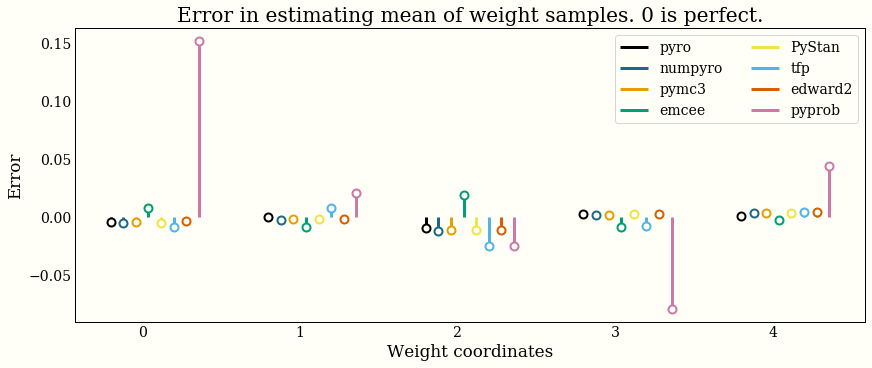
Accuracy

I have confidence that all the libraries implement their algorithm of choice correctly, and I tried to write a simple model that would provide some reasonable samples from the correct posterior. This section only tries to verify that my implementations are reasonable.

To say again with a stronger font, any errors shown here are (probably) MCMC error, and should not be interpreted as an implementation being "good" or "bad". It is a bigger, more careful job to benchmark performance, which is definitely not what this chart does.